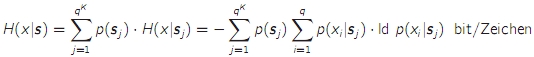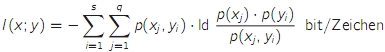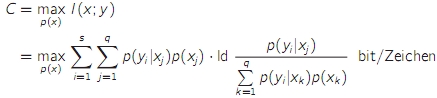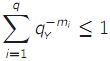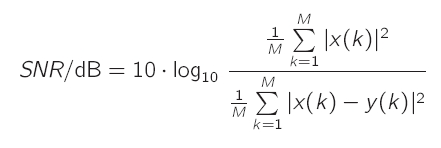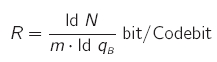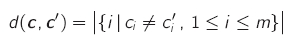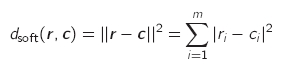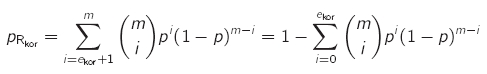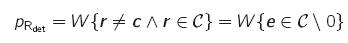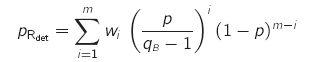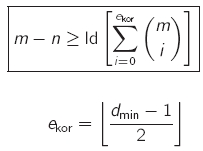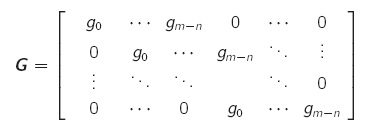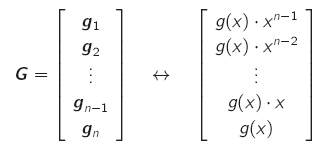Benutzer-Werkzeuge
Inhaltsverzeichnis
Informationstheorie und Codierung
Überblick
- Quellencodierung beseitigt Redundanz in der Nachricht
- Kanalcodierung fügt der Nachricht wieder Redundanz hinzu (z.B. zur Fehlerkorrektur)
Informationstheorie
- basiert auf grundlegenden Arbeiten von Shannon
- eine Quelle liefert informationskennzeichnende Zeichen xi aus einem q Zeichen umfassenden Alphabet X mit gewissen Wahrscheinlichkeiten
- bei stationäre Quellen sind die Wahrscheinlichkeiten, mit denen die Quelle Zeichen abgibt nicht von der Zeit abhängig
- bei gedächtnislosen Quellen sind die Wahrscheinlichkeiten der Zeichen unabhängig von zuvor oder im Anschluss gesendeten Zeichen
- aus den Elementen des Zeichenvorrats können Worte wi der Länge mi gebildet werden. Es lassen sich qm verschiedene Worte gleicher Länge m herstellen
- eine Codierung ist die Vorschrift zur eindeutigen Abbildung der Zeichen eines Zeichenvorrats A auf Codeworte, die aus den Zeichen eines Zeichenvorrats B gebildet werden: C(xi) = wi
- Beispiele für Codes: Morse-Code, ASCII-Code, Dezimal-, Oktalzahlen etc.
- Information ist Abbau von Ungewissheit (Beispiel Zufallsexperiment: Ausgang vorher unbekannt, danach bekannt)
- Informationsgehalt I(xi)/bit = -ld p(xi)
- I(xi, xj) = I(xi) + I(xj)
- der Informationsgehalt ist umso größer, je unwahrscheinlicher das Zeichen ist
- jedes Zeichen eines binären Zeichenvorrats hat bei gleichwahrscheinlichem Auftreten einen Informationsgehalt von -ld (0,5) = 1
- die Entropie H ist der mittlere Informationsgehalt der Zeichen einer Quelle → Maß für statistische Unordnung bzw. Unsicherheit
- die Entropie ist der Erwartungswert des Informationsgehalts
- die Entropie wird maximal, wenn alle Zeichen eines Zeichenvorrats gleich wahrscheinlich sind, Bezeichnung: Hmax oder H0
- die maximale Entropie wird auch als Entscheidungsgehalt einer Quelle bezeichnet
- der Unterschied zwischen H(x) und H0 wird als Redundanz bezeichnet: p = H0 - H(x)
- eine Redundanz kann auch für Codes angegeben werden: pcode = L - H(x) mit L = mittlere Codewortlänge
- relative Coderedundanz oder Weitschweifigkeit: (L - H(x)) / L, Codeeffizienz: H(x) / L
- ein optimaler Code besitzt unter bestimmten Randbedingungen (insb. ganzzahlige Wortlängen) die geringstmögliche Redundanz bzw. größtmögliche Effizienz
- eine Quelle, deren Gedächtnis K Zeichen in die Vergangenheit reicht, wird als Markov-Quelle K-ter Ordnung bezeichnet
- allg. Markov-Quelle = Markov-Quelle 1. Ordnung, gedächtnislose Quelle = Markov-Quelle 0. Ordnung
- die bedingte Entropie H(x|s) ist der Mittelwert (über alle Zustände) des mittleren Informationsgehalts eines Zeichens, das in einem bestimmten Zustand der Quelle abgegeben wird
- die bedingte Entropie kann nie größer werden als die "normale" Entropie
- die Verbundentropie (H(x,s) ist der mittlere Informationsgehalt von ganzen Ausgangsfolgen einer Markov-Quelle
- H(x,s) = H(x|s) + H(s) wobei H(s) wiederum eine Verbundentropie ist
- beim Erhöhen der Nachrichtenlänge nähert sich der mittlere Informationsgehalt pro Zeichen asymptotisch der bedingten Entropie
Übertragungskanäle
- abstraktes Kanalmodell des diskreten Kanals: x → Modulator → physikalischer Kanal → Demodulator → y
- die Aufgabe von Modulator und Demodulator ist es, einen möglichst guten diskreten Kanal zu bilden
- die Aufgabe von Codierer und Decodierer ist es, eine zuverlässige Übertragung über diesen Kanal zu gewährleisten
- Demodulationsverfahren
- Hard-Decision: Ein- und Ausgabealphabet sind identisch
- Soft-Decision: liefert kontinuierlich verteilte Ausgangswerte
- bei Kanälen mit Gedächtnis hängt die Wahrscheinlichkeit des Ausgangszeichens nicht nur vom Eingangszeichen ab, sondern auch von den K vorangehenden Zeichen
- diskreter gedächtnisloser Kanal = Discrete Memoryless Channel (DMC)
- die Kanalmatrix enthält die Wahrscheinlichkeiten für die Ausgangszeichen
- p(yj|xi) = Wahrscheinlichkeit, dass yj empfangen wird, wenn xi gesendet wurde
- die Zeilensummen müssen 1 ergeben: 1 = p(y1|xi) + p(y2|xi) + … + p(yj|xi)
- p(xj|yi) heißt A-posteriori-Wahrscheinlichkeit, p(xj) heißt A-priori-Wahrscheinlichkeit
- der Detektor schließt aus dem empfangenen Zeichen yi auf das gesendete Zeichen xj
- Maximierung der A-posteriori-Wahrscheinlichkeit (Maximum-A-Posteriori-Probability-Detektion: MAP-Detektion) p(yi|xj) * p(xj)
- wenn die Quellenstatistik nicht bekannt ist, fällt p(xj) weg bzw. ist für alle Eingangszeichen gleich. Dann wird lediglich das Maximum von p(yi|xj) gesucht → Maximum-Likelihood-Detektor
- Entropien im Kanal
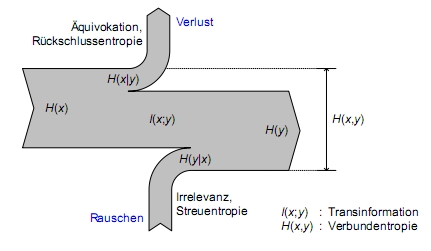
- die Verbundentropie des Kanals gibt den mittleren Informationsgehalt eines Ein-/Ausgangszeichenpaares an
- die bedingte Entropie H(x|y) heißt Rückschlussentropie oder Äquivokation und gibt den zusätzlichen Informationsgehalt eines Eingangszeichens an, wenn man das Ausgangszeichen kennt
- die bedingte Entropie H(y|x) heißt Streuentropie oder Irrelevanz und gibt den zusätzlichen Informationsgehalt eines Ausgangszeichens an, wenn man das Eingangszeichen bereits kennt
- H(x,y) = H(x|y) + H(y) = H(y|x) + H(x)
- die Transinformation I(x;y) ist ein Maß für die mittlere in einem Ausgangszeichen enthaltene relevante Information (mittlerer Informationsgehalt abzüglich Irrelevanz)
- I(x;y) = H(y) - H(y|x)
- Sonderfälle der DMC
- rauschfreier Kanal: Kanalmatrix hat in jeder Zeile nur einen Wert != 0
- verlustfreier Kanal: Kanalmatrix hat in jeder Spalte nur einen Wert != 0
- total gestörter Kanal: Ein- und Ausgangszeichen sind statistisch unabhängig voneinander
- symmetrischer Kanal: für die Elemente der Kanalmatrix gilt p(yi|xj) = 1 - p (Fehlerwahrscheinlichkeit des Kanals) wenn i = j, sonst = p / (q - 1)
- Sonderfall: Binary Symmetric Channel (BSC) und Binary Symmetric Erasure Channel (BSEC)
- die Kanalkapazität ist das Maximum der Transinformation für einen gegebenen Kanal
- bei symmetrischen Kanälen führen gleiche Wahrscheinlichkeiten der Eingangszeichen zur maximalen Transinformation und damit zur Kanalkapazität
Quellencodierung
- durch Codierung kann die Redundanz von Quellsymbolen verringert (Datenkompression) oder erhöht (Fehlerkorrektur) werden
- 2 Arten
- verlustlose Codierung → Reduzierung der Redundanz
- verlustbehaftete Codierung → Reduzierung der Irrelevanz
verlustlose Codierung
- ein Quellencodierer erzeugt aus Quellzeichen Codeworte
- die Gesamtheit der Codeworte heißt Code
- Codes mit gleicher Wortlänge für jedes Codewort heißen Blockcodes
- Klassen von Codes
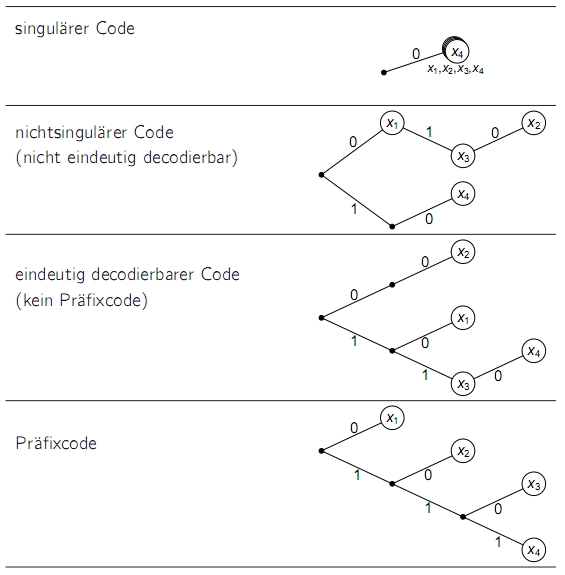
- nichtsinguläre Codes: eineindeutige (injektive) Abbildung zwischen Quellzeichen und Codewort (evtl. sind Trennzeichen zwischen den Codeworten nötig)
- eindeutig decodierbare Codes: jede Folge von Codewörtern kann eindeutig auf eine Folge von Quellzeichen abgebildet werden (evtl. müssen alle Codewörter gelesen werden, um das erste Quellzeichen decodieren zu können)
- unmittelbar decodierbare Codes, präfixfreie oder Präfixcodes: die Decodierung ist stets unmittelbar möglich, da kein längeres Codewort Anfangszeichen enthält, die einem kürzeren Codewort entsprechen)
- Codeeffizienz: H(x) / L (mit L = mittlere Wortlänge * ld q) oder H(y) / Hmax(y)
- ein eindeutiger Code mit der Effizienz 1 heißt idealer Code
- ein optimaler Code (bezogen auf eine gegebene Quelle mit H(x)) liegt vor, wenn es keinen anderen eindeutig decodierbaren Code mit kleinerer mittlerer Wortlänge L gibt. Ein idealer Code ist optimal
- die Codewortlängen eines jedes eindeutig decodierbaren Codes müssen die Kraft-McMillan-Ungleichung erfüllen
- Huffman-Codes
- einfaches Verfahren zur Erzeugung von optimalen Präfixcodes (mit minimaler mittlerer Codewortlänge)
- Entropie-Codierung: Quellzeichen mit geringer Wahrscheinlichkeit bekommen längere Codeworte zugewiesen
- Nachteile
- Übertragungsfehler wirken sich durch Fehlerfortpflanzung stark aus
- codierter Datenstrom ist nicht mehr synchron zum Quelldatenstrom
- Einsortieren der zusammengefassten Zeichen an jeweils höchster Stelle führt zu minimaler Varianz
- Fundamentalsatz der Quellencodierung oder Shannons 1. Satz: Für jede stationäre gedächtnislose Quelle gibt es einen Code, dessen Effizienz beliebig nahe bei 1 liegt.
- arithmetische Codierung: Codierung der gesamten Nachricht aus Quellzeichen mit bekannten Auftrittswahrscheinlichkeiten als reelle Zahl
- zustandsabhängige Codierung: anwendbar bei gedächtnisbehafteten Quellen, bei denen die Auftrittswahrscheinlichkeiten der Quellzeichen abhängig vom aktuellen Zustand sind
- abhängig vom aktuellen Zustand wird eine für diesen Zustand optimale Codetabelle verwendet → Codeumschaltung
- Lauflängencodierung: hier werden mehrfach hintereinander auftretende Quellzeichen in der Form {Zeichen, Anzahl} codiert
- Ausnutzung der Korrelation aufeinanderfolgender Zeichen
- Kompressionsverfahren mit adaptiven Wörterbüchern
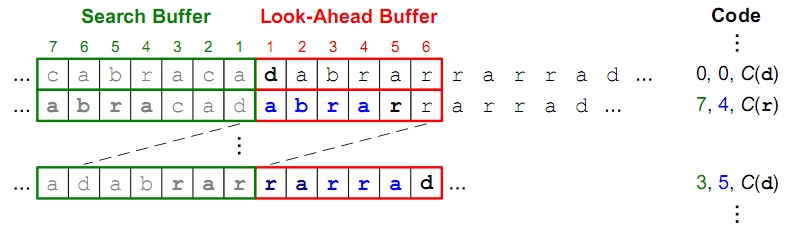
- LZ77: Sliding Window
- LZ78: Aufbau eines expliziten adaptiven Wörterbuches (Erweiterung des LZ77, bei dem Zeichenfolgen außerhalb des Search Buffer nicht erkannt werden)
- Problem ist das Finden der optimalen Wörterbuchgröße
- LZW: wie LZ78 nur mit Startwörterbuch, das alle Einzelzeichen des Quellalphabets enthält
verlustbehaftete Codierung
- bei verlustloser Codierung liegt der Schwerpunkt auf der Effizienz (Kompressionsrate), die begrenzt ist durch die Quellenentropie
- statt Verlusten sagt man auch Verzerrungen
- das Maß der Qualitätsbeeinträchtigung durch Verzerrungen muss vom jeweiligen Rezipienten bestimmt werden, da messbare Abweichungen nicht unbedingt mit der von Menschen empfundenen Qualität übereinstimmen
- einfache Berechnungen der Verzerrung ermitteln den (absoluten oder quadratischen) Abstand zwischen Eingangs- und Ausgangszeichen
- dabei ist es sinnvoll, den mittleren quadratischen Fehler dieser Abstände zu ermitteln (MSE = Mean Square Error)
* {{:se:mse.jpg|}}* das Signal-Verzerrungs-Verhältnis (SNR = Signal to Noise Ratio) setzt den Erwartungswert der quadratischen Eingangszeichen zu dem der Verzerrung ins Verhältnis
- um zeit- und wertkontinuierlichen Signale wie Sprache codieren zu können, müssen die diskretisiert werden
- die Diskretisierung zeitkontinuierlicher Signale erfordert immer eine Zeitdiskretisierung (Abtastung)
- eine verlustfreie Abtastung kann nur bei bandbegrenzten Signalen und ausreichend hoher Abtastrate gewährleistet werden (→ Nyquist-Theorem)
- diese Bandbegrenzung ist aber nicht immer gegeben, sodass meist eine Antialias-Tiefpassfilterung vorgenommen werden muss
* Antialiasing sorgt für eine Abschwächung des Alias-Effekts (zu hohe Frequenzen werden als niedrig abgetastet) * {{:se:aliaseffekt.jpg|}} * ein Tiefpassfilter schwächt zu hohe Frequenzen ab, sodass das Endsignal nur Frequenzen innerhalb eines bestimmten Bandes aufweist * Beispiel Telefonie: alle Frequenzen über 3,4kHz werden "abgeschnitten"* im Anschluss an die Abtastung müssen die ermittelten Werte quantisiert werden
* die Quantisierung bildet die kontinuierlichen oder fein quantisierten Ausgangswerte nicht umkehrbar auf diskrete Repräsentanten ab (Quantisierungsniveaus) * {{:se:quantisierung.jpg|}} * der Quantisierungsfehler kann als mit den Ausgangswerten unkorrelierte Zufallsvariable angesehen werden * die Quantisierungsintervalle können theoretisch beliebig und unterschiedlich groß sein, es bietet sich jedoch an, gleich große Intervalle zu bilden * {{:se:gleichmaessigequantisierung.jpg|}} * die Zahl der Quantisierungsniveaus ist in der Praxis immer endlich (2<sup>w</sup> mit w als Binärwortlänge für die codierten Stufen) * {{:se:quantisierungskennlinien.jpg|}} * {{:se:snrgleichmaessigerquantisierer.jpg|}} * bei Sprache ist die Verteilung der Frequenzen recht ungleich: viele kleine Signalwerte, wenig große. Daher muss die Quantisiereraussteuerung gering bleiben, was zu geringerem SNR führt * Gegenmaßnahmen: **ungleichmäßige Quantisierung** (unterschiedliche Quantisierungsstufenhöhen) oder **adaptive Quantisierung** (Anpassung des Quantisierers an momentane Größe der Eingangswerte)
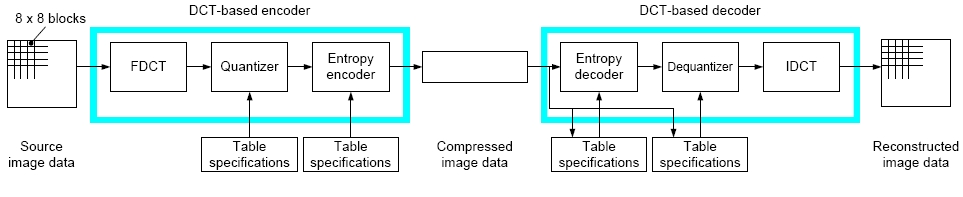
JPEG
- Verfahren zur Standbildkompression (ISO-Standard)
- nur Decodierprozess ist vorgeschrieben, nicht aber der Codierprozess
- der Baseline-Codec hat die Eigenschaften:
- Arbeitsweise auf Basis der Diskreten Cosinus-Transformation (DCT)
- Quellbild hat 8 bit pro Komponente (z.B. pro Farbe)
- Huffman-Codierung
- 2 verlustbehaftete Schritte: Subsampling und Quantisierung der DCT-Werte
* Farbraumtransformation - Bilder liegen meist in RGB-Darstellung mit 8 bit pro Farbe vor
- Berechnung der Helligkeitsinformationen (Luminanz) und Farbdifferenzinformationen (Chrominanz) und Darstellung in Form von YUV
- sinnvoll, da das menschliche Auge Helligkeitsunterschiede besser wahrnimmt als Farbunterschiede
- die Auflösung der Chrominanzwerte kann nochmal um den Faktor 2 verringert werden (Subsampling)
* die Codierung erfolgt im Frequenzbereich, wozu die Werte in diesen überführt werden müssen → DCT - die DCT-Werte stellen niedrige und hohe Ortsfrequenzen dar (sich langsam bzw. schnell verändernde Werteabfolgen in Zeilen- und Spaltenrichtung) bzw. die Ähnlichkeit der Blöcke mit den Basisfunktionen
- die Quantisierung der DCT-Werte bestimmt den Kompressionsfaktor
- die Quantisierung erfolgt gleichförmig, jedoch für jeden der 64 Koeffizienten mit einer in einer Quantisierungsmatrix festgelegten Stufenhöhe
- dabei werden die höherfrequenten Koeffizienten gröber quantisiert als die niederfrequenten, die letztere für die menschliche Wahrnehmung wichtiger sind
- Codierung der quantisierten DCT-Werte mittels Huffman-Codierung
- zuerst werden die Koeffizienten nach ihren Frequenzen sortiert (schlangenförmig von links oben nach rechts unten), sodass es zu längeren Nullfolgen (durch weniger hochfrequente Anteile in Bildern und zusätzlich die gröbere Quantisierung) kommt → Lauflängencodierung
- die DC-Werte (Wert des Pixels 1/1) werden als Differenz zum DC-Werte des Blocks links neben dem aktuellen Block angegeben (die Differenz hat eine geringere Korrelation als die DC-Werte selbst, und kann damit effektiver Huffman-codiert werden)
MP3
- bei der Audiokompression kann man Phänomene der Psychoakustik ausnutzen, um Irrelevanz (die der Empfänger nicht wahrnimmt) "abzuschneiden"
- Töne mit hohem Schalldruck (laute Töne) maskieren Töne in umliegenden Frequenzen, die einen geringeren Schalldruck aufweisen (Simultanverdeckung)
- auch kurz nach und interessanterweise auch vor dem Auftreten eines Maskierers verdeckt dieser Töne umliegender Frequenzen
- moderne Audiocodierverfahren basieren auf dem Ausnutzen der Maskierungsschwelle und einem dadurch möglichen größeren Rauschen, als dies beim klassischen Verfahren (CD) der Fall ist (weißes Rauschen)
- MP3 definiert nur codierten Bitstrom und Decoder-Algorithmus
- der Standard sieht Abtastraten von 32, 44.1 oder 48 KHz vor mit Bitraten zwischen 32 und 320 kbit/s
- ab ca. 160 kbit/s wird kein Unterschied mehr zwischen uncodiertem und codiertem Signal wahrgenommen
-
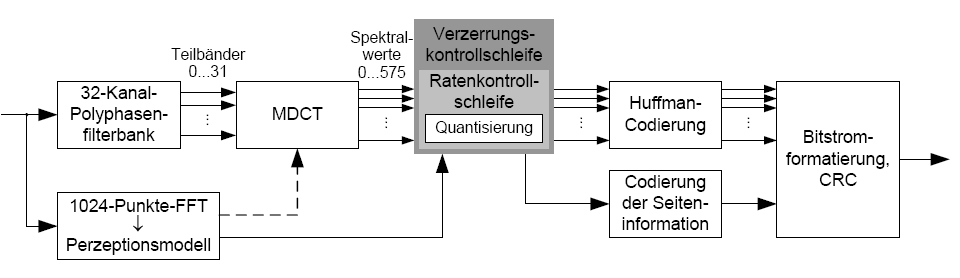
- die Polyphasen-Filterbank teilt das Signal in 32 Teilbänder, die danach noch mit MDTC in jeweils 18 Unterkanäle aufgeteilt werden → 576 Spektralwerte
- mittels FFT wird gleichzeitig das Perzeptionsmodell erstellt, das hauptsächlich die konkreten Verdeckungsschwellen als Ergebnis liefert
- die Quantisierung (zwei Schleifen) muss dafür sorgen, dass die Verzerrung in allen Kanälen unterhalb der Maskierungsschwelle bleibt
- dabei werden ungleichmäßige Quantisierer eingesetzt, die kleine Spektralwerte mit höherer Genauigkeit darstellen
- die quantisierten Spektralwerte werden Huffman-codiert (die häufigen kleinen Werte bekommen kurze Codewörter)
- die Bitrate wird iterativ angepasst
- die Spektralwerte können durch einen globalen Verstärkungsfaktor und Skalierungsfaktoren für bestimmte Bereiche des Spektrums abgeschwächt werden
- Funktionsweise: der globale Verstärkungsfaktor wird variiert und nach einer erneuten Quantisierung und Codierung überprüft, ob das Ergebnis der Ausgangsbitrate entspricht und die Maskierungsschwelle eingehalten wird (evtl. Korrektur durch Anpassung der Skalierungsfaktoren)
Kanalcodierung
- die Grundidee der Kanalcodierung ist die Vermeidung von Übertragungsfehlern oder die Erkennung der solchen durch gezieltes Hinzufügen von Redundanz
- FEC (Forward Error Control) und ARQ (Automatic Repeat Request)
- FEC wird verwendet, wenn es keinen Rückkanal gibt oder die Übertragungszeit für den Request und die Antwort zu lang wäre (z.B. Mobilfunk)
- bei PC-Netzen wird meist ARQ verwendet, da der Overhead hier keine große Rolle spielt und ARQ weniger aufwändig ist als FEC (bei gleicher Restfehlerwahrscheinlichkeit)
- Auswahl eines Kanalcodes abhängig von Fehlerverhalten, Bandbreite, Sendeleistung, Delay und Art der Daten (wichtige Daten brauchen bessere Absicherung)
- werden Nachrichten in geichgroße Blöcke aufgeteilt, handelt es sich um Blockcodes
- gibt es hierbei jedoch ein blockübergreifendes Gedächtnis, spricht man von Faltungscodes
- Coderate: Verhältnis von Infosymbolen zu Codesymbolen
- Hamminggewicht: Anzahl der von Null verschiedenen Symbole eines Codewortes
- die Gewichtsverteilung sind die Anzahlen der Codewörter mit Hamminggewicht 0…m
- Hammingdistanz: Anzahl der verschiedenen Symbole zweier Codewörter
- die minimale Hammingdistanz ist die kleinste Hammingdistanz zwischen zwei unterschiedlichen Codewörtern eines Codes
- Kurzbezeichnung für Blockcodes: (m, n, dmin)q
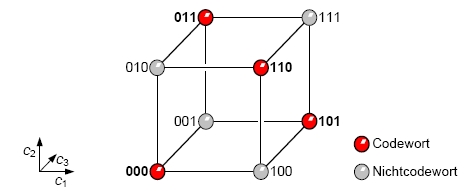
- der Coderaum umfasst alle m-stelligen Codewörter und dient u.a. der Darstellung von Distanzen zwischen den Codewörtern
- das Beispiel hat eine minimale Hammingdistanz von 2 und kann damit 1 Bitfehler bei der Übertragung erkennen
- mögliche Fehlererkennung: edet = dmin - 1
- mögliche Fehlerkorrektur: ekor = (dmin - 1) / 2 (abrunden)
- perfekter Code (dicht gepackter Code): alle Codeworte des Codes liegen in Korrigierkugeln mit einem Radius von ekor
- Decodierung: Hard-Decision (Empfangsworte stammen aus dem Codealphabet), Soft-Decision (Empfangsworte stammen aus einem größeren Alphabet)
- bei der Decodierung soll anhand des Empfangswortes das Wort gefunden werden, das mit der größten Wahrscheinlichkeit gesendet wurde
- Maximierung der A-posteriori-Wahrscheinlichkeit (MAP): p(c|r) bzw. p(u|r)
- wird auch Minimum Error Probability Decoding (MED) genannt, da die geringste Wortfehlerwahrscheinlichkeit erzielt wird
- Hard-Decision: das Codewort, das dem Empfangswort zugewiesen wird, ist dasjenige, welches die geringste Hammingdistanz zum Empfangswort aufweist
- Soft-Decision: Entscheidung aufgrund des Abstandsmaßes zwischen Codewort und Empfangswort (quadrierte euklidische Distanz im Coderaum)
- die feinere Quantisierung der Symbole des Empfangswortes führt zu einer geringeren quantisierungsbedingten Verfälschung und sorgt für eine Berücksichtigung der in den Symbolen enthaltenen Zuverlässigkeitsinformation
- um mittels Hard-Decision die gleiche Fehlerwahrscheinlichkeit zu erreichen wie mit Soft-Decision müsste man eine verdoppelte Sendeleistung aufwenden
- Interleaving: Methode zum Umgang mit Bündelfehlern (mehrere Fehler gleichzeitig: Fehlerbursts)
- die Codeworte werden ineinander verschachtelt, wodurch Bündelfehler sich zwar auf mehrere Worte, aber auf jedes einzeln nicht so stark auswirken
- Folge ist ein erhöhter Speicherbedarf und eine Übertragungsverzögerung
Lineare Blockcodes
- häufig verwendet: Modulo-2-Rechnung
- die Ergebnisse der Modulo-2-Addition und Modulo-2-Subtraktion entsprechen sich und dem Ergebnis einer XOR-Verknüpfung
- Definition: ein binärer (m,n)-Code ist ein linearer Blockcode, wenn er ein n-dimensionalen Unterraum des Coderaums {0,1}m im Sinn der Modulo-2-Rechnung ist
- jede beliebige Linearkombination aus Codewörtern ergibt wieder ein Codewort
- damit muss in jedem linearen Blockcode auch das Nullwort enthalten sein
- d(c,c') = w(c-c'), damit ergibt sich die minimale Hammingdistanz aus der Suche nach dem Codewort mit dem geringsten Hamminggewicht (außer dem Nullwort)
- als Restfehler wird bei Fehlerkorrektur mittels Kanalcodes die Falschkorrektur (das ermittelte Codewort entspricht nicht dem übermittelten) bezeichnet
- das empfangene Codewort wurde durch Verfälschung zu einem anderen gültigen Codewort
- bei linearen Blockcodes treten Restfehler genau dann auf, wenn der Fehlervektor ein vom Nullwort verschiedenes Codewort ist
- Singleton-Schranke: m - n >= dmin - 1
- Codes, die dies mit Gleichheit erfüllen, heißen MDS-Codes (Maximum Distance Seperable)
- Beispiele: (m,1,m)2-Wiederholungscodes, (n+1,n,2)2-Paritätscodes
- Hamming-Schranke / Kugelpackungsschranke (Sphere-Packing Bound)
- Codes, die dies mit Gleichheit erfüllen, heißen perfekte Codes oder dicht gepackte Codes (alle Worte liegen innerhalb von Korrigierkugeln)
- Beispiele für perfekte Codes: (m,1,m)-Wiederholungscodes mit ungeradem m
* Plotkin-Schranke * {{:se:plotkinschranke.jpg|}} * Codes, die dies mit Gleichheit erfüllen, heißen äquidistante Codes (alle Worte haben paarweise gleiche Abstände) * Gilbert-Varshamov-Schranke * {{:se:gilbertvarshamovschranke.jpg|}} * bei Erfüllung dieser Schranke kann auf die Existenz eines solchen Codes geschlossen werden (ohne jedoch eine Konstruktionsvorschrift anzugeben)* arithmetische Beschreibung linearer Blockcodes
- bei der Codierung werden aus den Infowörtern durch Multiplikation mit einer Generatormatrix Codewörter erzeugt
- die Generatormatrix besteht aus n Codewörtern der Länge m
* ein Vertauschen der Spalten der Generatormatrix erzeugt einen äquivalenten Code mit den gleichen Parametern (aber anderen Codewörtern) * ein Vertauschen der Zeilen oder das Ersetzen einer Zeile durch ihre Summe mit einer anderen Zeile ändert nicht den Code, sondern nur die Zuordnung von Codewörtern zu Infowörtern
* systematische Codes sind solche, bei denen die Infobits in allen Codeworten an der gleichen Stelle stehen (ergänzt um die Schutzbits), sie lassen sich also ohne Berechnung aus dem Codewort ablesen
- die Generatormatrix G hat dabei n Spalten mit jeweils nur einer 1
- Codewörter klar-systematischer Codes bestehen aus dem Infowort mit angehängten Schutzbits, d.h. die Infobits in Infowort und Codewort stehen an der gleichen Stelle
- die Generatormatrix weist hierbei die Zeilennormalform [En|P] auf (n x n Einheitsmatrix + n x (m - n) Matrix für die Prüfstellen)
- aus jedem linearen Blockcode kann durch Anwendung der Zeilenoperationen ein systematischer Blockcode gemacht werden
- einen klar-systematischen (äquivalenten) Code erhält man dann ggfs. durch Spaltenvertauschung
- Decodierung mittels Prüfmatrix H = [PT|Em - n]
- das Syndrom eines Empfangswortes ist s = r * HT und muss für alle Codeworte 0 sein
- ist es ungleich 0 kann auf einen Übertragungsfehler geschlossen werden und das wahrscheinlichste Codewort ermittelt werden
- hierzu wird aus der Nebenklasse der Fehlermuster mit gleichem Syndrom dasjenige mit dem kleinsten Hamminggewicht ausgewählt und zum Empfangswort addiert
- Modifikation linearer Codes
- Expandieren: m' > m, n' = n, R' < R, d'min >= dmin
- Punktieren: m' < m, n' = n, R' > R, d'min ⇐ dmin
- Verlängern: m' > m, n' > n, m' - n' = m - n, R' > R, d'min ⇐ dmin
- Verkürzen: m' < m, n' < n, m' - n' = m - n, R' < R, d'min >= dmin
- wenn Codes durch Vertauschen der Generator- und Prüfmatrix ineinander übergehen (z.B. Paritäts- und Wiederholungscode), nennt man diese Codes dual oder orthogonal
- Hamming-Codes sind Einzelfehler-korrigierende Blockcodes, deren Coderate mit wachsender Blocklänge gegen 1 geht
- Hamming-Codes können erstellt werden, indem die 2m - n - 1 von 0 verschiedenen Paritätsbit-Kombinationen in Spaltenform angeordnet und dann so sortiert werden, dass rechts eine m-n x m-n Einheitsmatrix entsteht. Aus dieser Prüfmatrix kann nun die Generatormatrix des Hamming-Codes abgeleitet werden.
- bei zyklische Blockcodes, die eine Untermenge der linearen Blockcodes sind, entstehen auch durch zyklische Verschiebung der Codeworte (z.B. um 1 nach links: 010001 → 100010) andere Codeworte
- Vorteil: können einfach mittels rückgekoppelten Schieberegistern (LFSR = Linear Feedback Shift Register) realisiert werden
- fehlererkennende zyklische Blockcodes (CRC = Cyclic Redundancy Check) erkennen gut Bündelfehler
- wenn ein Generatorpolynom bekannt ist, kann damit durch c(x) = u(x) * g(x) der (meist nicht-systematische) Code erzeugt werden
- Codeworte sind daher immer Vielfache des Generatorpolynoms
* die Syndrome bei zyklischen Blockcodes entspechen s(x) = r(x) mod g(x) * ein Fehler ist aufgetreten, wenn der Rest dieser Division nicht 0 ist * ein zyklischer Code ist durch die Angabe seines Generatorpolynoms und der Codewortlänge vollständig definiert * ein zyklischer Code entsteht, wenn zu einem gegebenen Generatorpolynom eine Codewortlänge gewählt wird, die der Zykluslänge entspricht * größere Zykluslängen führen zu einer höheren Coderate * wenn die Zykluslänge eines Polynoms den maximalen Wert 2<sup>k</sup> - 1 annimmt, handelt es sich um ein **primitives Polynom** (es ist dann auch irreduzibel)
* (Bündel-)Fehlererkennung durch zyklische Blockcodes
- von einem Bündelfehler der Länge t spricht man, wenn innerhalb eines Codeabschnitts der Länge t maximal t Fehler auftreten
- Bündelfehler können sich auch zyklisch vom Wortende zum Anfang erstrecken, dann werden sie zyklische Bündelfehler genannt
- zyklische Blockcodes erkennen mindestens Einzelfehler, Doppelfehler und Bündelfehler bis zur Länge k = m - n
- spezielle zyklische Codes
- zyklische Hamming-Codes: werden aus primitiven Generatorpolynomen erzeugt
- Fire-Codes: verwenden ein Produkt g(x) = g1(x) * (xk2 + 1) aus zwei irreduziblen Polynomen als Generatorpolynom
* BCH-Codes (Bose-Chaudhuri-Hocquenghem) erlauben die Korrektur von zufällig verteilten Fehlern * RS-Codes (Reed-Solomon) bilden eine Klasse von nichtbinären BCH-Codes * gehören zu den besten bekannten Bündelfehler-korrigierenden Codes (z.B. Audio-CD)
Faltungscodes
- Faltungscodes haben ein Blockübergreifendes Gedächtnis und können mit sehr kleinen Blöcken (oft n = 1) arbeiten
- werden z.B. beim Mobilfunk eingesetzt
- man kann recht einfach auch den ungleichmäßigen Schutz der Nachrichtenbits erreichen (wichtige Bereiche werden besser geschützt)
* der Entwurf erfolgt nicht algebraisch, sondern durch rechnergestützte Suche * Unterscheidung in rekursiv/nicht-rekursiv und systematisch/nicht-systematisch * häufig: Nonrecursive nonsystematic Convolution (NSC)
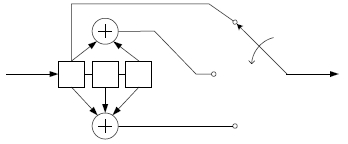
- das Beispiel macht aus einem Eingangsbit drei Ausgangsbit, die der Reihe nach gesendet werden
- die Länge der Verzögerungskette (3 Bits gehen in die Berechnung ein) nennt man Einflusslänge (Constraint Length)
- das Gedächtnis ist die die Anzahl der vorangehenden Bits in der Verzögerungskette (Anzahl - 1)
* {{:se:schaltbildfaltungscodiererallgemein.jpg|}}* Darstellungsformen
- grafisch (s.o.)
- Koeffizientenmatrix, in der die Einsen dafür stehen, dass das entsprechende Eingangsbit in die Modulo-2-Operation zur Ermittlung des Ausgangsbits eingeht
- die Matrixzeilen (Generatoren) werden häufig in Oktalschreibweise angegeben
- Baumdiagramme
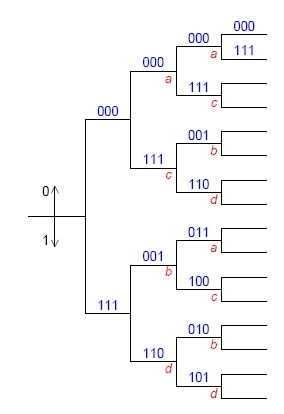
* Zustandsdiagramme * {{:se:zustandsdiagrammfaltungscodierer.jpg|}} * Trellisdiagramme: Zustanddiagramme, in denen die neuen Zustände immer nach rechts weiter abgetragen werden * {{:se:trellisdiagramm.jpg|}} * erst nach 2 Schritten können alle Zustände erreicht werden (eingeschwungener Zustand)* Decodierung
- die Decodierung erfolgt mittels des Viterbi-Algorithmus, also der Suche nach dem am besten übereinstimmenden Pfad des Trellisdiagramms
- Zweigdistanz/Zweigmetrik für jeden Zweig ermitteln (unterschiedliche Bits zur Eingangsfolge bei Hard-Decision, euklidische Distanz bei Soft-Decision) - die Zweigdistanz wird zur Survivormetrik des Ursprungsknotens des Zweiges addiert -> neue Summenzweigmetrik/Summenmetrik - die neue Survivormetrik des Zielknotens ergibt sich als Minimum aller Summenzweigmetriken der in den Knoten mündenden Zweige. Diese Survivormetriken werden für alle Knoten berechnet. - die Survivorpfade ergeben sich durch Rückverfolgen (Backtracing) des Pfades, der den Zweig mit der minimalen Summenzweigmetrik enthält * {{:se:viterbi1.jpg|}} * {{:se:viterbi2.jpg|}} * {{:se:viterbi3.jpg|}}* analog zur Hammingdistanz kann man bei Faltungscodes eine Minimaldistanz dfree (freie Distanz) als kleinstes Gewicht der Pfade vom Nullzustand in den Nullzustand (ohne reinen Nullpfad)
Klausur
Wichtige Feststellungen und Definitionen
- Entropie: mittlerer Informationsgehalt der Zeichen des Quellalphabets
- Gleichverteilung der Symbolwahrscheinlichkeiten ⇒ maximale Entropie (Entscheidungsgehalt) H0 = ld(q)
- bedingte Entropie: mittlere Entropie aller Zustände
* H(x|s) ≤ H(x)
* Verbundentropie: mittlerer Informationsgehalt von Ausgangsfolgen einer Quelle
- Wahrscheinlichkeiten
- A-posteriori p(x|y)
- A-priori p(x)
- Äquivokation/Rückschlussentropie/Verlust H(x|y)
- Irrelevanz/Streuentropie/Rauschen H(y|x)
- Transinformation: mittlere im Ausgangszeichen eines Kanals enthaltene Information
- Kanalkapazität: Maximum der Transinformation
- bei symmetrischen Kanälen führt eine Gleichverteilung der Wahrscheinlichkeiten der Eingangszeichen zur maximalen Transinformation
- Zusammenfassen von Eingangssymbolen zu Eingangsfolgen erhöht die Codeeffizienz (1. Fundamentalsatz der Quellencodierung)
- arithmetische Codierung geht nur für stationäre gedächtnislose Quellen
- Ausnutzen von bedingten Wahrscheinlichkeiten bei Markov-Quellen erhöht die Effizienz
- Codeumschaltung: bei zustandsabhängiger Codierung wird je nach Zustand eine andere Codetabelle verwendet
- Lauflängencodierung ist nur sinnvoll, wenn genügend Zeichenfolgen auftreten, die in der Darstellung (Code, Lauflänge) kürzer sind als normal
- Verfahren mit adaptiven Wörterbüchern eignen sich auch für nicht-stationäre Quellen
* Blockcodes teilen die Nachrichten in gleichgroße Blöcke auf - um bei einem Gausskanal mittels Hard-Decision die gleiche Wortfehlerwahrscheinlichkeit erreichen wie mit Soft-Decision braucht man die doppelte Sendeleistung
- lineare Blockcodes: n < m, 2n Codeworte
- Wortfehler/Restfehler: aus dem Empfangswort wird auf das falsche Codewort geschlossen oder beim Korrigieren eines Fehlers wird das falsche Codewort erzeugt
* für kleine Bitfehlerwahrscheinlichkeiten resultiert ein Wortfehler meist aus der Verfälschung zu einem Codewort mit der zum korrekten Codewort minimalen Hammingdistanz
* Modifikationen (Expandieren, Punktieren, Verlängern, Verkürzen) führen systematische Codes wieder in systematische Codes über
- CRC-Codes sind fehlererkennende zyklische Blockcodes
- mit größeren Zykluslängen sind höhere Coderaten möglich
- primitives Polynom: die Zykluslänge entspricht dem maximalem Wert 2k - 1 und ist irreduzibel
- primitive Generatorpolynome erzeugen Codes mit dmin = 3
- meist werden CRC-Codes aus Generatorpolynomen der Form gprim(x) * (x + 1)
- dann: dmin = 4, z = 2k - 1 - 1
- jeder lineare Blockcode (auch zyklische Codes) enthält das Nullwort
Berechnungen
- Redundanz: ρ = H0 - H(x)
- Coderedundanz/Weitschweifigkeit pCode = L - H(x) (mit L = mittlere Wortlänge in Bit)
- relative Coderedundanz: pCode<sub>rel</sub> = pCode / L
- Codeeffizienz η = H(x) / L
- Coderate R = m / n
- Entropie einer Markov-Quelle ohne Berücksichtigung der statistischen Bindung
- "normale" Entropie mit p(xi) berechnen
- bedingte Entropie bei gegebener Markov-Quelle
- p(xi|s) sind gegeben durch Zustandsdiagramm
- p(s) für alle Zustände ermitteln (lineares Gleichungssystem)
- H(x|s) für jeden Zustand ermitteln und mit p(s) multiplizieren und aufaddieren
- Verbundentropie
- bei Markov-Quellen
- Formel mit p(x,s) = p(x|s) * p(s)
- H(x,s) für n Zeichen = (n - 1) * H(x|s) + H(x)
- bei statistisch unabhängigen Ausgangszeichen: n * H(x)
- zyklische Blockcodes
- Generieren
- vollständig definiert durch Generatorpolynom und Codewortlänge (n = Rang des Generatorpolynoms)
- g(x) und n gegeben (oder aus m ermittelt) → alle Permutationen von Wörtern der Länge n mit g(x) multiplizieren
- systematische Codes: Permutationen der Länge n erzeugen, d(x) = u(x) * xk mod g(x) addieren
- Generatormatrix erzeugen
- Koeffizienten eintragen und n Mal verschieben → Streifenform
* zyklische Hamming-Codes: Erzeugen durch primitive Generatorpolynome
- Fire-Codes: Erzeugen durch Produkt zweier irreduzibler Polynome
* minimale Hammingdistanz durch Prüfmatrix ermitteln: jede Auswahl von dmin - 1 Spalten ist linear unabhängig und es gibt mindestens eine Auswahl von dmin linear abhängigen Spalten
Eigenschaften
- Code
- optimal/kompakt: größtmögliche Effizienz bei gegebener Quelle → kleinste mittlere Wortlänge
- ideal: eindeutig decodierbarer Effizienz η = 1
- eindeutig decodierbar: Erfüllen der Kraft-McMillan-Ungleichung
- perfekt/dicht gepackt: alle Worte eines Coderaums liegen in Korrigierkugeln mit Radius ekor, Hamming-Schranke wird mit Gleichheit erfüllt
* äquivalent: Codes mit gleichen Parametern m, n, d<sub>min</sub> und w * Code und Leistungsfähigkeit können abweichen, aber Distanzeigenschaften bleiben gleich * Erzeugen durch Vertauschen von Spalten in der Generatormatrix * systematisch: alle Eingangsbits stehen in allen Codeworten an der gleichen Stelle * klar-systematisch: die Eingangsbits stehen der Reihe nach am Anfang der Codeworte * Hamming-Codes: Coderate geht mit wachsender Blocklänge gegen 1 * Erzeugung: alle Permutationen von m - n Schutzbits als Spalten einer Prüfmatrix eintragen * Hamming-Schranke mit Gleichheit erfüllt * sind perfekt * äquidistant: Codeworte haben paarweise jeweils gleiche Abstände d<sub>min</sub>, Plotkin-Schranke mit Gleichheit erfüllt * identisch: Codes bestehen aus denselben Codeworten (nicht unbedingt in derselben Zuordnung zu Eingangsworten) * zyklisch: Codeworte gehen durch Verschiebung ineinander über
* Quelle
- stationär: Wahrscheinlichkeiten der Ausgabezeichen sind unabhängig von der Zeit
- gedächtnislos: Wahrscheinlichkeiten der Ausgabezeichen sind unabhängig von Zeichen davor/danach
- Kanal
- diskret: zeit- und wertdiskret
* symmetrisch: Anzahl Eingänge = Anzahl Ausgänge, Fehlerwahrscheinlichkeit p * verlustfrei/ungestört: nur ein von 0 verschiedener Eintrag je Spalte in der Kanalmatrix, aus Ausgangszeichen kann sicher auf das Eingangszeichen geschlossen werden * rauschfrei: Kanalmatrix ist quadratische Einheitmatrix, in jeder Zeile nur ein von 0 verschiedener Eintrag, 1 Eingangszeichen -> 1 Ausgangszeichen * total gestört: Ein- und Ausgangszeichen sind statistisch unabhängig, Transinformation = 0
* zyklische Blockcodes
- Codewortlänge muss gleich der Zykluslänge sein
* Zykluslänge z = kleinstes i, für das gilt: x<sup>i</sup> + 1 mod g(x) = 0 * Fehlererkennung: Einzel-, Doppel- und Bündelfehler bis zum Grad von g(x) sicher, darüber hinaus mit hoher Wahrscheinlichkeit * Fehlerkorrektur * primitives g(x): d<sub>min</sub> = 3 -> e<sub>kor</sub> = 1 * g(x) = g<sub>prim</sub>(x) * (x + 1): d<sub>min</sub> = 4 -> e<sub>kor</sub> = 1 * g(x) = g<sub>1</sub>(x) * (x<sup>k<sub>2</sub></sup> + 1) (Fire-Codes): d<sub>min</sub> = 4, sie können aber Bündelfehler korrigieren: t<sub>max</sub> ≤ k<sub>1</sub>, t<sub>max</sub> < k<sub>2</sub> / 2 + 1
ToDo
- Shannon-Grenze
- Wann welche Codierung? arithmetisch bei gedächtnisbehaftet?
- Gleichförmige Quantisierung
- Beispiele machen
* Huffman Code * Arithmetische Codierung * Lempel Ziv
* Kanalkapazität berechnen
- Kraft-McMillan
- Gewichtsverteilung berechnen
- Syndrome berechnen
- Decodierung der verschiedenen Codes
- zyklisch
- Polynomdivision
- Zykluslänge bestimmen